Теория игр: понятие, виды, применение

Сформулированный ещё в середине прошлого века математический термин давно вышел за рамки экономики и нашёл применение во всех сферах человеческой жизни: от выбора обеда до рабочих вопросов и воспитания детей. Им пользуются биологи, эксперты по искусственному интеллекту, психологи и даже военные.

Что это такое?

Теория игр – метод определения оптимальной стратегии в играх, где игра – это взаимодействие двух или более противостоящих сторон, преследующих собственные интересы.

В ситуациях, которые описывает теория игр, у участников есть по несколько вариантов действий, и все они влияют на других. Задача каждого участника – выбрать лучшую для себя стратегию в условиях такой гонки. Приведём пример.

Ситуация: на улице град, вы опаздываете на работу, и у вас есть два варианта пути: метро и ваш автомобиль.

На метро не влияет погода, оно едет быстро и по установленному расписанию, а машина может попасть в пробку. Вы уверены, что доберётесь вовремя, если выбирете метро. Но тут оказывается, что ещё сотни жителей вашего района подумали так же, и из-за толкучки вам пришлось пропустить один состав и опоздать. А ваш коллега, выбравший поездку на своём авто, приехал вовремя.

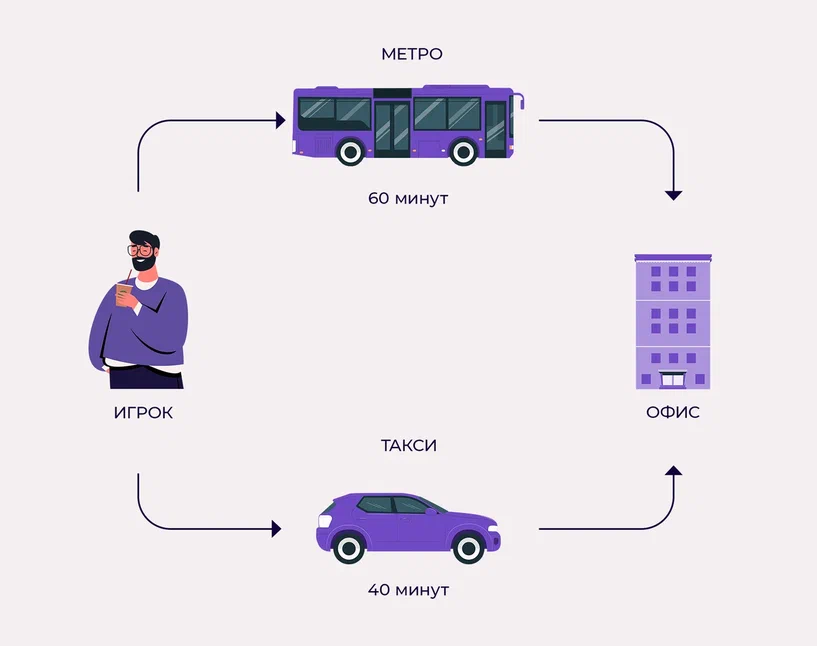
Оба варианта не могут вместить всех, а игроки не могут скооперироваться друг с другом.

Другие люди не знали, что выберете вы, также как и вы не знали, как поступят они. Всем оставалось только гадать, и как раз в том, чтобы предугадать действия соперника и на их основе выстроить стратегию для своей победы, и заключается теория игр.

Основные игры теории игр

Мы разобрались, что в играх есть соперники с одной целью и ограниченными ресурсами. Какие ещё критерии подразумевает теория игр?

1. В игре есть общие правила;
2. У каждого участника есть несколько вариантов действий, каждый из которых повлияет на других;
   
3. Все участники рациональны, и выбирают лучший для себя вариант на основе информации о действиях других участников.
   

В этом определении есть один минус: люди не всегда рациональны, да и не всегда рациональность идёт на пользу. Это прекрасно демонстрирует одна из основных проблем в теории игр – дилемма бандита (заключённого).

Дилемма бандита

Полиция поймала с поличным двух преступников примерно в одно и то же время, и подозревает их в сговоре. Для выяснения правды их разделили и предложили сделку:

• Если один сдаёт другого, то первого освобождают, а второй получает 10 лет заключения;
• Если оба сдают друг друга, оба получают по два года;
  
• Если оба молчат, оба получают по полгода за мелкое преступление.
  

Для каждого по отдельности лучшая стратегия – предательство, но, поскольку их двое, им стоит объединиться и выбрать последний вариант, чтобы обоим достался минимальный срок. Но они разделены, и никто из них не знает, как поступит другой, а лучший вариант “молчать” ведёт к риску получить 10 лет тюрьмы.

Поэтому оба стремятся обезопасить себя и сдают друг друга, и это и есть доминирующая стратегия – преследование только своих интересов, не думая о других. Дилемма бандита наглядно показывает, что иногда стоит быть эгоистом.

Доминирующая стратегия – та, что ведёт игрока к выигрышу. Строго доминирующая стратегия – та, что ведёт игрока к выигрышу вне зависимости от действий других игроков.

Доминирующие стратегии могут играться вместе и уравновесить друг друга, чтобы сделать оптимальным положение всех игроков. Никто не проигрывает и не выигрывает за счёт другого, хотя у обоих есть такие варианты: это называется равновесием Нэша. То есть, когда все игроки выбирают оптимальную для всех, но не лучшую для себя стратегию.

Джон Форбс Нэш – американский математик, получивший нобелевскую премию за свой вклад в развитие теории игр.

В нашем случае равновесие Нэша случится, если оба бандита выберут молчание. Оба могут сознаться и выбрать лучшие для себя условия, но не делают этого в пользу общего благополучия.

Дилемма бандита в жизни

1. Цены на рынке

Два соседних магазина могут договориться и вместе повысить цены, получив больше прибыли. А может повысить только один – и при одинаковом количестве клиентов заработать больше. Но если разница в цене будет слишком большой, все клиенты могут уйти в магазин подешевле, и в итоге больше прибыли получит он.

Если брать шире, и рассматривать не отдельные магазины, а целые компании, то изменение цен без координации с остальными неизбежно влияет на весь рынок. Компания с более низкими ценами получит большой доход, а второй придётся отвоёвывать свою долю рынка обратно.

2. Военное дело

Практически та же схема применима к, например, гонке вооружений. У нас есть страны А и Б:

• Если вооружатся обе страны – плохо, но не худший исход для обеих стран;
• Если вооружится одна из стран – выигрышно для одной, катастрофично для другой;
  
• Если не вооружится никто – лучший исход, но каждая из них всё ещё может вооружиться и встать в более выигрышную позицию.
  

Такие ситуации происходят практически во всех общественных сферах: экономике, информатике, социологии, бизнесе даже в повседневной жизни. Эта стратегическая теория игр объясняет и помогает их решить так, чтобы все остались в плюсе.

Задача справедливого деления торта

Торт с различными украшениями нужно разделить на n человек, но всем хочется кусочек с чем-то определённым. Кому-то нравится крем, кому-то вишенки, а кому-то просто хочется кусок побольше. Задача состоит в том, чтобы деление было справедливо, и каждый в равной степени получил то, что хочет.

Загадка, в которой равновесие Нэша – цель и единственный правильный ответ.

Существует множество способов деления. Вот несколько основных:

1) Дели-и-выбирай

Самый простой метод, которым мы сами часто пользуемся: торт делится на равные куски, и каждый участник выбирает тот, который ему нравится больше. С тортом этот метод сработает, но что, если участников много и все хотят тот самый кусочек с кремом? Вряд ли такой способ можно назвать справедливым.

2) Последний уменьшивший

Участник 1 отрезает кусок торта, который кажется ему справедливым, и передаёт его остальным. Участник 2 может согласиться с ним и пасовать (передать следующему), а может, если ему кажется, что это слишком много, обрезать его. Допустим, он пропускает и кусок передаётся участнику 3. Участник 3 считает кусок несправедливо большим и обрезает его. Обрезанная часть возвращается обратно в торт, а кусок достаётся тому, кто его обрезал. Если все участники посчитали кусок справедливым и ничего с ним не сделали, он достаётся участнику 1.

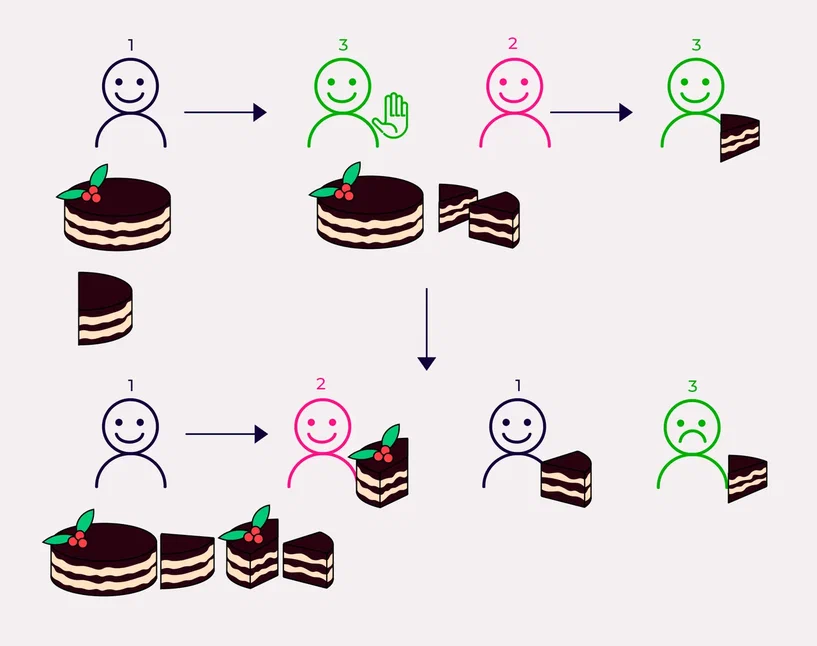
Так поступают со всеми кусками, пока не останутся два участника. Для них оставшийся торт делится уже по принципу дели-и-выбирай, и каждый выбирает тот кусок, который ему нравится.

Но что, если участнику 3, выбывшему на первом раунде, чужие куски понравятся больше? Опять выходит несправедливо. Поэтому существует следующий способ:

3) Метод Селфриджа-Конвея

Участник 1 делит торт на три равных куска. Затем участник 2 может либо пасовать, либо обрезать самый большой, по его мнению, кусок так, чтобы все куски были равны. Допустим, он обрезает его, а обрезки пока откладывает в сторону. Участник 3 выбирает себе понравившийся кусок из трёх равных, после него выбирает участник 2, и оставшийся достаётся участнику 1.

Затем на три равные части делятся обрезки, и каждый выбирает из них понравившийся: сначала участник 2, затем участник 1, и оставшийся уходит участнику 3.

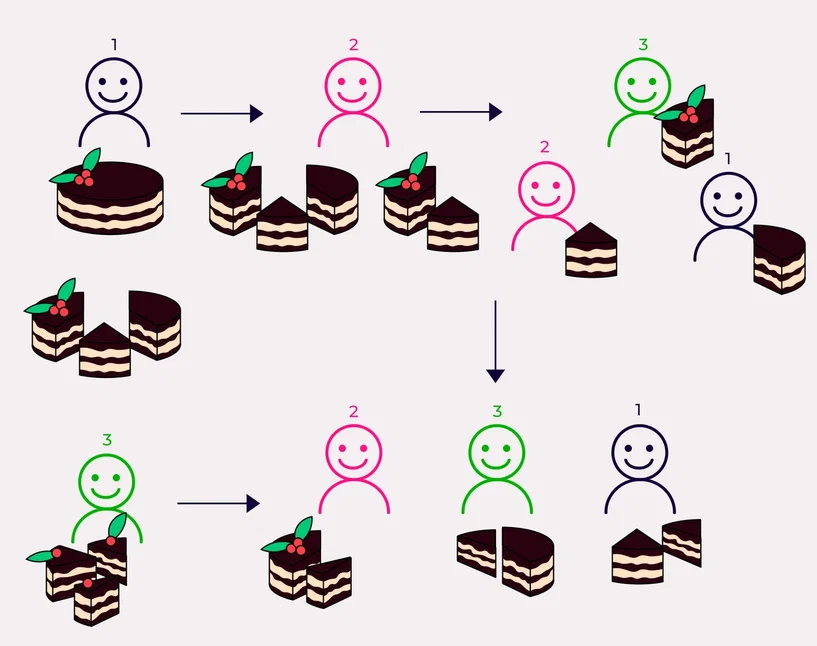
Способ разрезания торта для большего количества участников, основанный на этом методе, называется “движущийся нож”. Его главный минус – чем больше участников, тем больше разрезов.

Справедливое деление торта в жизни

Люди делят не только торты, но и земельные участки, рекламные билборды и обязанности работников. В делении работы по дому среди членов семьи, часов работы и даже наследства тоже применяется эта задача. Её уже почти век решают математики и информатики именно потому, что она имеет так много практических применений и не устаревает.

Практика теории игр: примеры

Во всех этих задачах присутствует мощный математический аппарат – вычислять вероятности и делить можно очень долго, и этим до сих пор активно занимаются учёные. 

Чаще всего она встречается и используется в:

• Политике: сложные общественно-политические процессы легко представить в таблицах, просчитать риски и предугадать, как и какие действия повлияют на другие партии, движения и страны.
• Бизнесе: как мы писали выше, теория игр здесь – основной инструмент планирования доходов компании, заключения сделок и принятия решений.
• IT: теория игр помогает обучать нейросети работать с людьми, другими нейросетями и большими данными.
• Биологии: изучение эволюции и поведение животных (а в психологии – человека) в зависимости от разных факторов.
• Жизни: сами не зная, мы используем теорию игр, когда выбираем место для отдыха, фильм на вечер, что сказать в разговоре и как поступить в ситуации. 

В целом теория игр – отличный инструмент для разработки стратегий и планирования действий в любых социальных проблемах, с которым мы часто сталкиваемся в повседневной жизни.

Теорию игр на практике поможет проверить школа программирования CODDY. Мы учим создавать игры, прокачиваем логику и раскладываем по полочкам точные науки. Переходите по ссылке и обучайтесь играя вместе с CODDY!